광추적기의 기본 구조
- pixel에 색 입히기
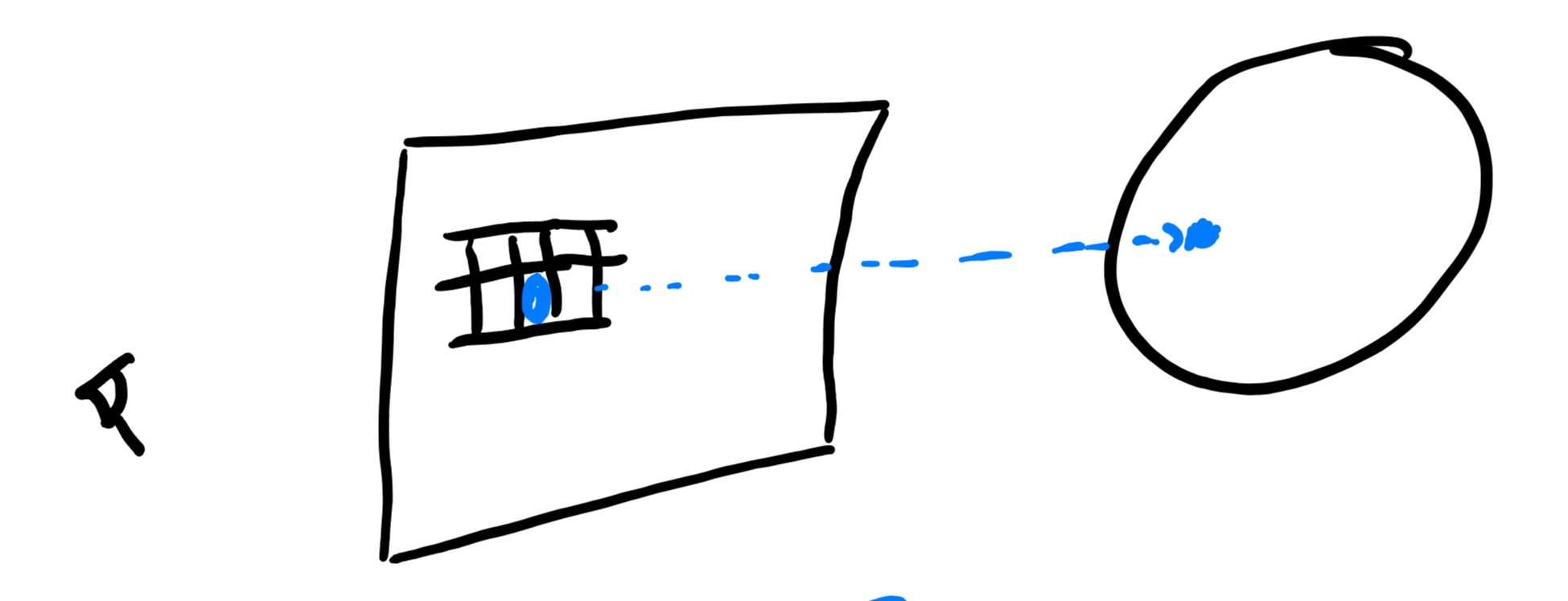
- pixel에 색을 입히기 위해선 눈에서부터 화면으로, 화면에서 가상의 물체로 ray를 쏜다고 가정해보자
- 이때 pixel의 z 방향으로 ray가 나간다 했을 때 ray는 물체에 충돌을 하거나 하지 않을것이다
- 충돌을 했다면 충돌 지점에 대한 색을 가져오고, ray를 쏜 pixel을 그 색으로 그려주면 물체의 색으로 물체가 화면에 그려지게 된다
- raytracing Render
void Render(std::vector<glm::vec4> &pixels) { std::fill(pixels.begin(), pixels.end(), vec4{0.0f, 0.0f, 0.0f, 1.0f}); #pragma omp parallel for for (int j = 0; j < height; j++) for (int i = 0; i < width; i++) { const vec3 pixelPosWorld = TransformScreenToWorld(vec2(i, j)); // 광선의 방향 벡터 // 스크린에 수직인 z방향, 절대값 1.0인 유닉 벡터 // Orthographic projection (정투영) vs perspective projection (원근투영) const auto rayDir = vec3(0.0f, 0.0f, 1.0f); Ray pixelRay{pixelPosWorld, rayDir}; // index에는 size_t형 사용 (index가 음수일 수는 없으니까) // traceRay()의 반환형은 vec3 (RGB), A는 불필요 pixels[size_t(i + width * j)] = vec4(traceRay(pixelRay), 1.0f); } }
- 모든 pixel에 대해 ray를 그리기 위해선 스크린 좌표계에서 현 위치를 월드로 변환해야 하는데 이는 TransformScreenToWorld에서 해줄것이다
- 이후 ray가 나갈 방향을 정해줘야 하는데, ray는 이번 실습에선 +z으로 나가 구현할 것이다
- 이 두 정보를 Ray 객체에 저장해주고, traceRay 함수를 통해 충돌된 물체의 색을 가져와 현재 pixel에 저장할 것이다
- traceRay
vec3 traceRay(Ray &ray) { const Hit hit = sphere->IntersectRayCollision(ray); if (hit.d < 0.0f) { return vec3(0.0f); } else { return sphere->color * hit.d; // 깊이를 곱해서 입체감 만들기 } }
- traceRay 함수는 ray를 가져와 우리가 그릴 물체와 충돌을 했는지 안했는지를 판단해 색을 return해주는 함수이다
- hit.d, 즉 distance가 0보다 작으면 충돌하지 않은것이므로 검은색을, 그렇지 않으면 물체의 색과 hit.d를 곱해 깊이감에 따른 색을 조절하여 입체감을 만들어 return해준다
실습
- hit된 물체 처리
- 물체가 선에 hit됐는지를 판단하기 위해서 사용할 방법중 하나로, 원과 직선의 충돌을 이용할 것이다(원을 그리고 있기 때문)
- 참고 자료: https://en.wikipedia.org/wiki/Line%E2%80%93sphere_intersection
- 참고자료를 보면 구의 방정식과 선에대한 방정식이 있는데 이들을 이용해 선의 원점으로부터의 거리를 구하면 충돌을 알 수 있다
- 이 두 방정식을 합쳐 d를 기준으로 정렬하면 2차 방정식을 구할 수 있는데, 이를 통해 d에대한 근의 공식을 유도하면 $-(\frac{b}{2}) \pm sqrt(\nabla)$라는 것을 알 수 있다
- 이때 $\nabla = [u \dot (o-c)]^2 - (||o - c||^2 - r^2)$으로 $nabla$가 0보다 작으면 충돌하지 않고, 0과 같으면 한 점에서 충돌, 0보다 크면 두점에서 충돌을 했다는 의미이다
- 두 점에서 충돌을 했을 때 두개의 distance를 구해 더 작은 값을 hit에 저장해주면 된다
- 그 이유는 투명하지 않은 물체는 두 지점중 앞에 충돌한 지점만을 그리고, 나중에 충돌한 지점은 앞에 충돌한 지점에 의해 가려질 것이기 때문이다
- 구현
Hit IntersectRayCollision(Ray &ray) { Hit hit = Hit{-1.0f, vec3(0.0f), vec3(0.0f)}; // d가 음수이면 충돌을 안한 것으로 가정 //const float a = glm::dot(ray.dir, ray.dir); // dir이 unit vector라면 a는 1.0f라서 생략 가능 const float b = 2 * glm::dot(ray.dir, (ray.start - center)); const float c = glm::dot(ray.start - center, ray.start - center) - (radius * radius); const float n = b * b /4.0f- c; if(n >= 0) { const float d1 = -b/2.0f + sqrt(n); const float d2 = -b/2.0f - sqrt(n); hit.d = min(d1, d2); // 광선의 시작점으로부터 충돌지점까지의 거리 (float) hit.point = ray.start + hit.d * ray.dir;// 광선과 구가 충돌한 지점의 위치 (vec3) hit.normal = glm::normalize(hit.point - center);// 충돌 지점에서 구의 단위 법선 벡터(unit normal vector) /* */ } return hit; }- 구현된 함수를 보면 a는 단위 벡터이므로 생략이 가능하고, b와 c를 참고 문서에 맞게 구한 뒤 $\nabla$인 n을 구해준다
- 이때 b에는 2가 곱해져 있지만 n을 구할 땐 b에서 2가 빠진 값을 연산하므로 b에 곱해진 2를 없애주기 위해 4를 곱해준다
- 구한 n이 0보다 작으면 초기 설정한 hit를 그대로 return하고, 그렇지 않다면 hit.d, hit.point, hit.normal을 구해 return해준다
- 결과
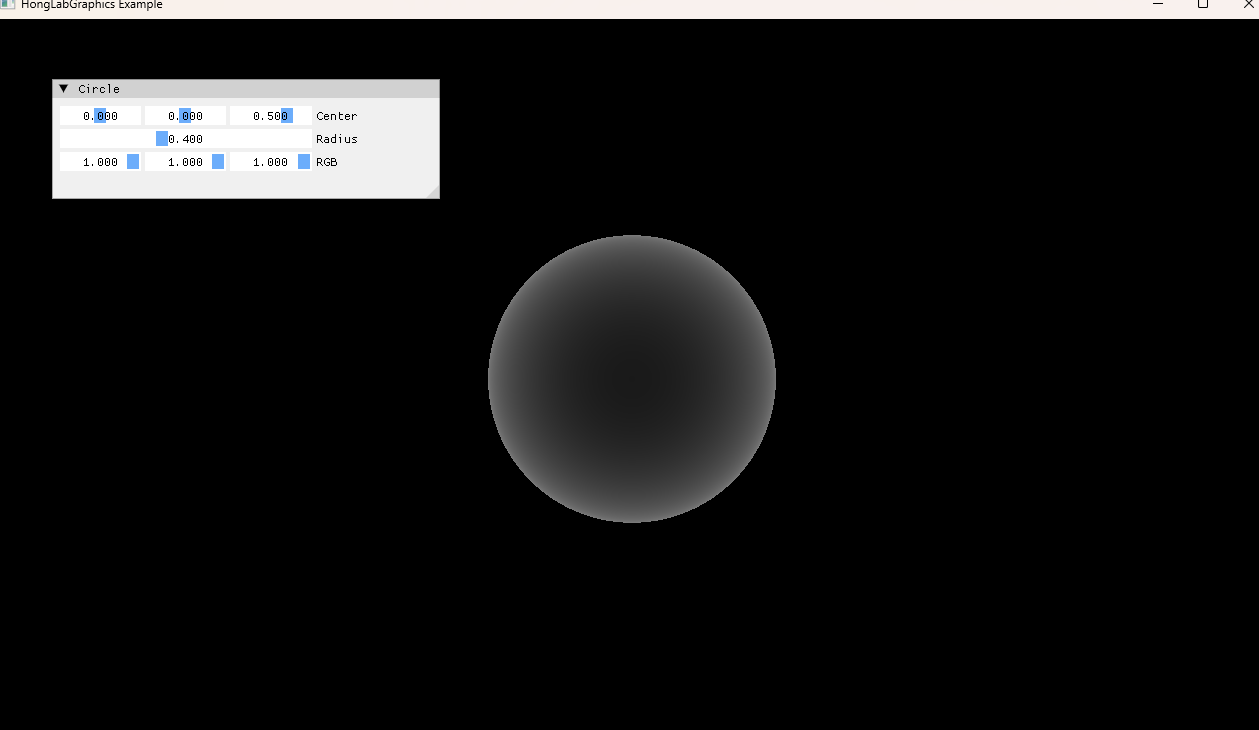
- 결과를 보면 깊이에 따라 색이 변하는 원을 그릴 수 있다
- 하지만 Z값이 변경되면 원이 앞뒤로 움직이면서 원근감이 생겨야 하는데 전혀 그렇지 않는 것을 볼 수 있다
- 이는 ray를 쏘는 방향이 (0,0,1)로 z 방향으로 만 쏘기 때문인데, 이는 정투영(Orthographic projection)으로 그리는 방법이기 때문이다
