인접 리스트
인접 리스트란
2차원 배열이 아닌 연결 리스트를 여러개 사용해서 만든 그래프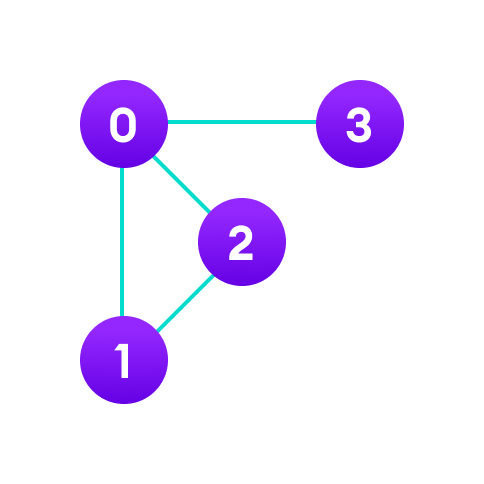
이 그래프를 인접 리스트를 사용하면 밑의 리스트처럼 나타낼 수 있다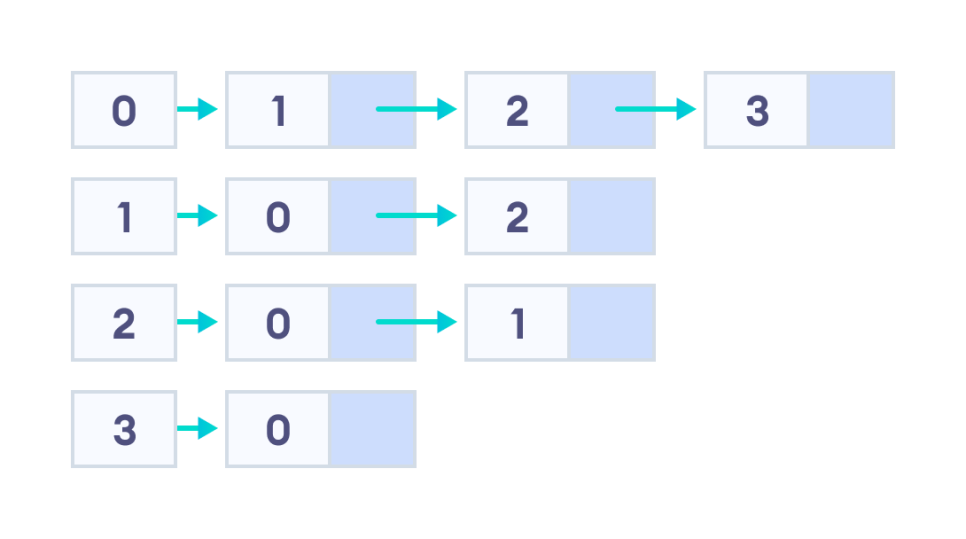
코드로 나타내기
#include<iostream>
#include<vecetor>
using namespace std;
const int V = 4;
vector<int> adj[V];
int main()
{
adj[0].push_back(1);
adj[0].push_back(2);
adj[0].push_back(3);
adj[1].push_back(0);
adj[1].push_back(2);
adj[2].push_back(0);
adj[2].push_back(1);
adj[3].push_back(0);
for(int i = 0; i < 4; i++)
{
cout << i << " :: ";
for(int there : adj[i])
cout << there << " ";
cout << '\n';
}
// 이렇게도 할 수 있다.
for(int i = 0; i < 4; i++)
{
cout << i << " :: ";
for(int j = 0; j < adj[i].size(); j++)
cout << adj[i][j] << " ";
cout << '\n';
}
}
/*
0 :: 1 2 3
1 :: 0 2
2 :: 0 1
3 :: 0
*/
[출처] [알고리즘 강의] 2주차. 그래프이론, 인접행렬, 인접리스트, DFS, BFS, 트리순회|작성자 큰돌list가 아닌 vector를 사용한 이유
list
- n번째 인덱스 삽입 삭제 : O(1)
- 마지막 요소에 삽입 삭제 : O(1)
- 특정 요소 탐색 : O(n)
- n번째 요소 참조 : O(n)
vector
- n번째 인덱스에 삽입 삭제 : O(n)
- 마지막 요소에 삽입 삭제 : O(1)
- 특정 요소 탐색 : O(n)
- n번째 요소 참조 : OP(1)
인접 리스트를 구현할 때 많이 사용되는 연산은 마지막 요소에 삽입과 해당 배열을 탐색하는 연산이기 때문에 vector로 구현해도 무방함
따라서 vector나 list 편한것으로 구현해도 무방
예시 문제
Q. 인접리스트를 기반으로 탐색하기
1번.
정점은 0번 부터 9번까지 10개의 노드가 있다. 1 - 2 / 1 - 3 / 3 - 4 라는 경로가 있다. (1번과 2번, 1번과 3번, 3번과 4번은 연결되어있다.)
이를 인접리스트로 표현한다면?
2번.
0번부터 방문안한 노드를 찾고 해당 노드부터 방문, 연결된 노드를 이어서 방문해서 출력하는 재귀함수를 만들고 싶다면 어떻게 해야할까? 또한, 정점을 방문하고 다시 방문하지 않게 만드려면 어떻게 해야할까?
[출처] [알고리즘 강의] 2주차. 그래프이론, 인접행렬, 인접리스트, DFS, BFS, 트리순회|작성자 큰돌#include<iostream>
#include <vector>
using namespace std;
const int length = 10;
vector<vector<int>> list(length);
bool visited[length];
void Go(int index)
{
cout << index << endl;
visited[index] = true;
for (int data : list[index])
{
if (visited[data] == false)
Go(data);
}
}
int main()
{
list[1].push_back(2);
list[1].push_back(3);
list[2].push_back(1);
list[3].push_back(1);
list[3].push_back(4);
list[4].push_back(3);
for (int i = 0; i < length; i++)
if (list[i].size() != 0 && visited[i] == false)
Go(i);
}'코딩 태스트 > 개념' 카테고리의 다른 글
| 맵과 방향 벡터(Direction Vector) (0) | 2025.01.10 |
|---|---|
| 인접 행렬과 인접 리스트 차이 (0) | 2025.01.10 |
| 인접행렬(Adjacency Matrix) (0) | 2025.01.10 |
| 이진 탐색트리(BTS, Binary Search Tree) (1) | 2025.01.10 |
| 이진트리(BT, Binary Tree) (0) | 2025.01.10 |
