행렬(Row Column)
- 행렬과 상수 곱셈
- 행렬*상수 = 행렬에 속한 값에 각각 상수를 곱해주면 된다
- 행렬의 덧셈 뺄셈
- 행렬끼리의 덧셈 뺄셈은 동일한 행, 렬을 가진 포멧에서만 가능
- 동일한 행,렬에 속하는 값끼리 계산해주면 된다
- 행렬끼리 곱
- 앞에 오는 행렬의 렬의 갯수와 뒤에 오는 행렬의 행의 갯수가 같아야한다
- 앞에오는 행렬의 행 * 뒤에오는 열 을 곱하는 방식으로 각각 구해진다
- 행렬과 상수 곱셈
행렬의 법칙
- 교환법칙
- 정의
- 연산의 위치를 바꿔도 동일한 값이 나와야한다
- 행렬은 곱셈이나 나눗셈은 연산하는 행렬의 순서가 바뀌면 값이 달라지므로 성립하지 않는다
- 정의
- 결합법칙
- 정의
- 연산의 순서를 바꿔도 결과가 같다
- 행렬은 결합법칙이 성립한다
- 정의
- 교환법칙
항등행렬(Identity)
- 정의
- 모든 값들이 0이지만 행과 열이 같은 애들은 1인 값
- 2x2 행렬 = 1 0
0 1
- 항등 행렬과 다른 행렬 A와 곱하면 위치 상관없이 항상 A 행렬이 나온다
- 정의
역행렬
- 정의
- 행렬 A에 어떠한 행렬을 곱했을 때 항등행렬 I가 나오는 행렬
- A라는 행렬에 변화를 줄건데 그 변화를 뒤로돌려 상쇄시키고 싶을 때 많이 사용
- 항상 존재하지 않는다
- 역행렬이 존재하려면 D = ad - bc != 0 이 참이여야 한다
- 역행렬 공식
- A 행렬의 역행렬 -> $A^{-1}$ = 1/D * d - b
-c a
- A 행렬의 역행렬 -> $A^{-1}$ = 1/D * d - b
- 정의
전치 행렬
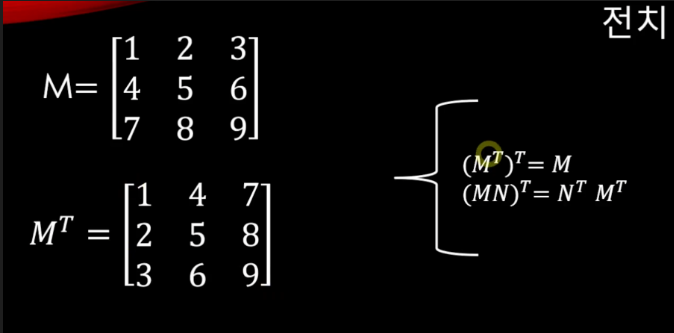
- 정의
- 행렬의 대각선을 기준으로 서로의 위치를 바꾸는 행렬
- 정의
직교 행렬
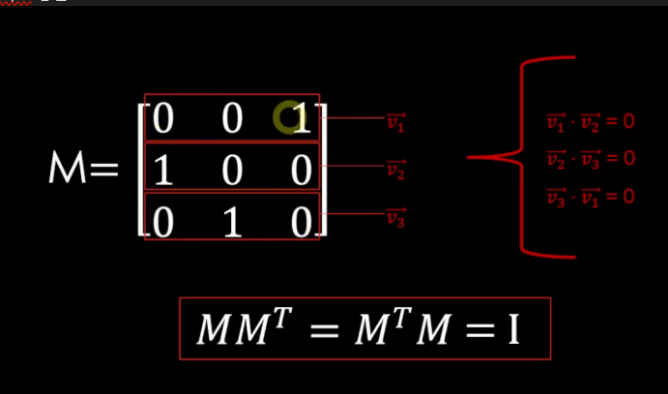
- 정의
- 각 성분들이 직각인 행렬
- 내적을 통해 알아볼 수 있음
- 직교 행렬에 직교 행렬의 전치 행렬을 곱해주면 항등행렬 I가 나온다
- 즉 직교 행렬의 역행렬은 전치 행렬이다
- 정의
내적 - 외적
- 내적
- 정의
- 두 벡터가 이루는 각도를 활용해 벡터 간의 관계를 계산하는 방법
- 두 벡터가 얼마나 같은 방향으로 가는지 유사성을 측정하는데 사용
- 결과는 스칼라 값
- 수식 : A⋅B=∣A∣∣B∣cosθ (θ 는 두 벡터사이 값)
- 두 벡터가 같은 방향일 때 내적값은 최대
- 서로 직각일 때 내적 값 0
- 반대 방향일 경우 음수
- 용도
- 벡터간 유사도
- 광원계산
- 물체의 표면과 카메라 시점이 얼마나 일치하는지 계산
- 정의
- 외적
- 정의
- 두 벡터로 부터 세번째 벡터를 생성하는 연산
- 새로운 벡터는 두 벡터와 수직인 방향을 갖는다
- 결과는 벡터 값
- 수식 : A×B=(AyBz−AzBy,AzBx−AxBz,AxBy−AyBx)
- 두 벡터에 모두 수직인 새로운 벡터 생성
- 벡터의 크기는 두 벡터가 이루는 평행사변형의 면적과 같다
- 용도
- 법선 벡터 계산
- 물리 회전
- 물리 시뮬레이션에서 토크 계산
- 삼각형의 면 법선(normal)을 구해 빛의 반사 방향
- 표면에 수직인 벡터를 구하는데 사용
- 정의
- 내적
벡터와 행렬
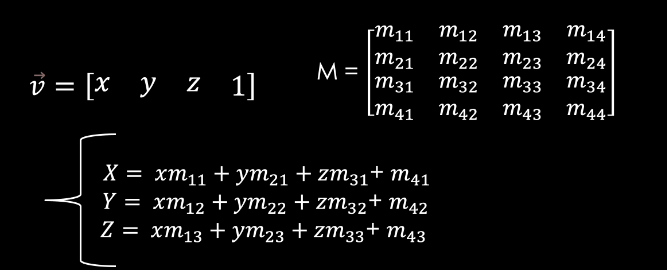
- 벡터와 행렬의 곱을 이용하여 각각의 좌표 등등을 구할 수 있다
'DirectX' 카테고리의 다른 글
| 12 좌표계 변환 행렬 (0) | 2025.01.12 |
|---|---|
| 11 SRT 변환 행렬 (0) | 2025.01.12 |
| 08 1주차 복습 (0) | 2025.01.12 |
| 07 Rasterizer State, Sampler State, Blend State (0) | 2025.01.12 |
| 06 Constant Buffer (1) | 2025.01.12 |
